자료구조 트리(Tree) 이해하기

트리는 그래프 중에서 특정조건을 가진 형태의 자료구조를 의미한다.

면접에서 트리의 정의에 대해서 질문을 받게되면, 싸이클이 존재하지 않는 방향 그래프(DAG, Directed Acyclic Graph)라고 대답하면 거의 맞는 대답이다.

자세한 이야기는 그래프에서 다루기로 하자.

 

실생활에서 트리구조를 어렵지 않게 찾아볼수 있는데, 그 중에 하나의 예시로 조직도가 있다.

 

위의 조직도 예시에서처럼 대표이사> 총괄임원 > 팀 > 부문 의 계층적 구조를 가진 형태를 트리라고 할수 있다.

컴퓨터공학의 자료구조 관점에서는 상위노드를 부모노드, 아래노드를 자식노드라고 정의하고 있다.

 

트리의 이론적 정의
A tree consists of a root, and zero or more subtrees T1, T2, … , Tk such that there is an edge from the root of the tree to the root of each subtree. 

Introduction to Tree - Data Structure and Algorithm Tutorials

주요 트리 용어

- 기본적으로 위의 그림을 보면 각 용어의 의미는 파악할 수 있을 것이다.

• Root Node(루트 노드) : 부모가 없는 노드, 트리는 하나의 루트 노드 만을 가진다.
• Leaf Node(단말 노드) : 자식이 없는 노드(=Terminal Node)
• Edge(간선) :  노드를 연결하는 선
• Subtree : 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
• Silbing(형제) : 같은 부모를 가지는 노드
• Degree of Node(차수) : 각 노드에서 뻗어나온 가지의 수
• Height of Tree(높이) : Root Node로 부터 Leaf Node까지의 간선의 최대값(가장 깊숙한 노드의 깊이)

트리의 특징

• 부모 자식 관계가 존재하는 계층형 모델이다
• 방향성이 존재하고, 싸이클이 존재하지 않는 비순환이다.
• 트리 순회의 종류는 전위순회, 중위순회, 후위순회, 레벨 순회가 있다.

트리의 종류

 이번 글에서는 기본적인 트리의 종류인 편향 트리, 이진트리에 대해서 간단하게 소개정도만 하려고 한다.

• 편향 트리(Skew tree)
• 이진 트리(Binary Tree)
• 이진 탐색 트리(Binary Search Tree, BST)
• m원 탐색 트리(m-way search tree)
• 균형 트리(Balanced Tree, B-Tree)
• 레드-블랙 트리(Red-Black Tree, RB tree)

---

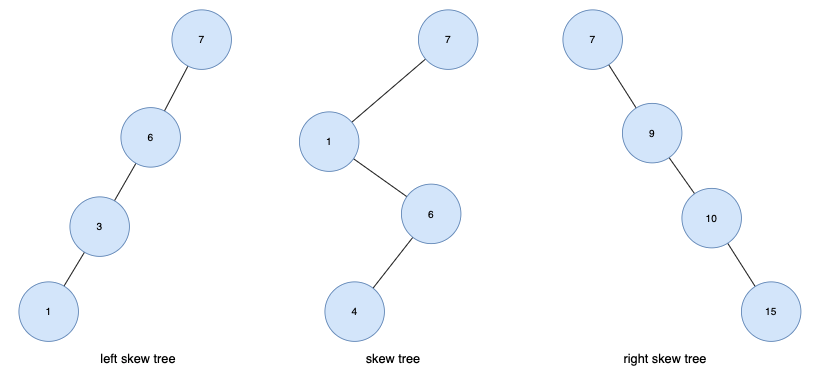
편향트리(skew tree)

 모든 노드들이 자식을 하나만 갖는 트리를 편향 트리라고 한다.

자식을 갖는 방향에 따라 skew tree, left-skew tree, right-skew tree로 구분된다.

skew tree 종류

---

이진트리

트리 중에서 각 노드의 자식노드가 0~2개인 트리를 이진트리(Binary Tree)라고 한다.

• 이진트리 유형
  1) 전 이진트리(Full Binary Tree/Strict Binary Tree)
  2) 완전 이진트리(Complete Binary Tree)
  3) 포화 이진트리(Perfect binary Tree)
  4) 균형 이진 트리(Balanced Binary Tree)
• 이진트리 관련 용어
  1) Node A의 높이(Height) : A의 자속 노드 중 가장 멀리 떨어진 Leaf Node까지의 거리
  2) Tree B의 높이(Height) : Root Node의 높이로 정의
• 이진트리 특징
  1) 이진 트리의 레벨 k(k는 1부터 시작)에서의 노드 수의 최대는 2^(k-1)
  2) 높이 h인 트리의 최대 노드의 수는 2^k-1

 

 

 이번 글에서는 기본적인 트리의 종류인 편향 트리, 이진트리에 대해서 간단하게 소개정도했는데, 앞으로 작성하는 글에 자세한 설명을 추가해서 설명해보려고 한다.